An incorrect way that might seem obvious is just to subtract inflation rate from your interest rate. E.g., if you gain 15%, and inflation is 5%, then subtract 5 from 15 to get a yield of 10%. That doesn't actually work.
Consider that simple example and look at the actual numbers:
The difference here is maybe easiest to understand by considering how much of an item you can buy. Say an item costs $100 today, and you have $100. You can buy exactly one of those items ($100/$100 = 1).
Now, say you invested that $100. You got 15% on your investment somehow, and inflation was 5%. After 10 years, you have $405 (1.15^10) and the item costs $163 (1.05^10). You can now buy ($405/$163) = ~2.5 of the items. If you were to do this by subtracting the inflation rate from the yield, you'd have $260 (1.1^10) so you could buy ~2.6 of the items.
Taking away the specific numbers, the effective power of the money from that example is:
where t is the doubling time and r is the effective yield. Combining this with Equation 2 then gives you the actual doubling time:
You can just plug in numbers that you want. I've put a few examples below:
Now, say you invested that $100. You got 15% on your investment somehow, and inflation was 5%. After 10 years, you have $405 (1.15^10) and the item costs $163 (1.05^10). You can now buy ($405/$163) = ~2.5 of the items. If you were to do this by subtracting the inflation rate from the yield, you'd have $260 (1.1^10) so you could buy ~2.6 of the items.
Taking away the specific numbers, the effective power of the money from that example is:
 |
| Equation 1: This is the correction equation |
Simplified a bit if you prefer, that's:
 |
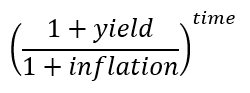| Equation 2: This is a simplified version of the correct equation |
If you represent the 'yield - inflation' method above, you get this:
 |
| Equation 3: This is the incorrect equation |
Those two are not equivalent.
Now...to actually calculate the doubling time. The equation above gives you the effective yield. Referring to the previous post on this, we found:
 |
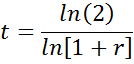| Equation 4 \ |
where t is the doubling time and r is the effective yield. Combining this with Equation 2 then gives you the actual doubling time:
 |
| Equation 5 |
You can just plug in numbers that you want. I've put a few examples below:
| gain % | inflation % | doubling time (years) |
| 5 | 0 | 14.2 |
| 5 | 2 | 23.9 |
| 8 | 0 | 9.0 |
| 8 | 2 | 12.1 |
| 10 | 0 | 7.3 |
| 10 | 2 | 9.2 |
Important note...remember that rates are often given in %. Thus, an 8% yield means the yield in the equations above is 0.08.
0 comments:
Post a Comment