Calculator
Initial Amount ($)
Investment Yield (%)
Retirement Yield (%)
Defer Years
Monthly Payout ($)
Payment Years
Inflation (%)
Required Monthly Deposit ($)
Required Monthly Deposit ($)
Derivation
I haven't actually seen this solved anywhere else online so I'm posting the full math behind this since it took me a couple of hours to get right and was a fun problem. A number of places have very simplified versions of it, but none that I found included the investment, the payout, and the inflation. Note that no one reviewed this so I might have typos, and feel free to let me know in the comments if I do.
The basic problem being solved here is finding the monthly input that makes the future value of an investment at the end of the defer period equal to the present value of the payout at the end of the defer period:
 |
| PVout = present value of the payouts at the end of the defer period FVin = future value of the total investments at the end of the defer period |
First, we need to figure out how to calculate those. Start with the future value of the investment.
We have an initial investment that's the 'Initial Amount' in the calculator. That will grow at the 'Investment Yield' for the entire defer period. Its value at the end of the defer period is simply:
 |
| PVo = initial investment yin = investment yield per month t = months in defer period |
Next, we have the future value of the monthly investments. This is the hardest one to calculate and I was unable to come up with a simple equation for it. To start with, you want the value at the end of the defer period of the first two months. That's:
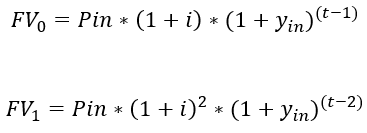 |
| FV = future value of the term Pin = amount invested each month in today's dollars i = monthly inflation rate yin = monthly investment yield t = months in defer period |
This continues and thinking about it all the way through the defer period, you end up with:
 |
| Pin = amount invested each month in today's dollars i = monthly inflation rate r = monthly investment yield t = months in defer period |
I don't know how to simplify this summation any further so we're left with this:
Finally, we move to the present value of the payout at the end of the defer period. Do like before and take the first couple of months then write the general sum:
 |
| Pout = monthly payment t = months in defer period n = months in payout period yout = monthly retirement yield i = monthly inflation rate |
Noting that t and i are constants, we can pull those out and get:
 |
| PVout = present value of payout at end of defer Pout = monthly payment t = months in defer period n = months in payout period yout = monthly retirement yield i = monthly inflation rate |
This is a Geometric Series and it has a known sum grouping the terms like the following:
 |
| see the link for definitions of a and r here |
 |
| PVout = present value of payout at end of defer Pout = monthly payment t = months in defer period n = months in payout period yout = monthly retirement yield i = monthly inflation rate |
Now...plugging all of this into the very first equation and solving for Pin, you end up with:
This is the math behind this problem. It's worth noting that minor changes to this can give you things like:
- how to calculate the yield of an annuity, including with inflation
- how to calculate the yield required to get a given retirement amount
- how much you end up with if you invest a given amount of money each month












🎰 รวมเกมสล็อตสุดปัง แตกง่าย ได้เงินชัวร์
ReplyDelete🃏 คาสิโนไลฟ์ ทุกรูปแบบ จริงใจ โปร่งใส การันตี💯%
⚽️ กีฬาต่างๆ ทั่วโลก🌎 ราคาน้ำดีคอมมิชชั่นสูง 💥
⭐️ฝาก-ถอน ไม่มีขั้นต่ำ ไม่ต้องทำเทิร์น
🔥 มาลุ้นโบนัสนาทีทองได้แล้วในเวลานี้
📱ทุนน้อย แตกหนักกันรั่วๆๆ ถอนกำไรเน้นๆ 💵
💸 ฝาก 20 ถอน 1,000+++ ปังไม่ไหว แตกันหนักๆๆรัวๆ
🧏 แอดมินให้บริการ รวดเร็ว ทันใจ